Ultrastrong Capacitive Coupling of Flux Qubits

Authors: Hita-Perez, Maria; Jauma, Gabriel; Pino, Manuel; Garcia-Ripoll, Juan Jose

Journal: PHYSICAL REVIEW APPLIED

Publication date: 2022/01/24

DOI: 10.1103/PhysRevApplied.17.014028

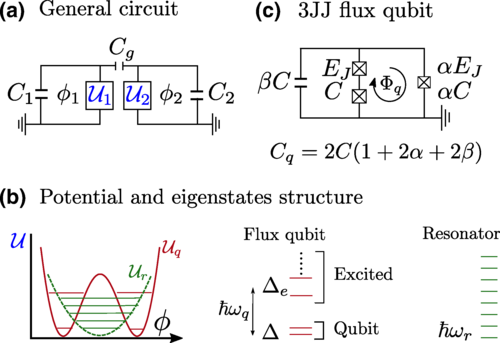
Abstract: A flux qubit can interact strongly when it is capacitively coupled to other circuit elements. This interaction can be separated into two parts, one acting on the qubit subspaces and one in which excited states mediate the interaction. The first term dominates the interaction between the flux qubit and an LC resonator, leading to ultrastrong couplings of the form sigma(y)(a + a dagger), which complement the inductive sigma(x)i(a dagger – a) coupling. However, when coupling two flux qubits capacitively, all terms need to be taken into account, leading to complex nonstoquastic ultrastrong interaction of types sigma(y)(1)sigma(y)(2), sigma(z)(1)sigma(z)(2), and sigma(x)(1)sigma(x)(2). Our theory explains all these interactions, describing them in terms of general circuit properties-coupling capacitances, qubit gaps, inductive, Josephson and capacitive energies-that apply to a wide variety of circuits and flux qubit designs.